Conjuntos numéricos

Introducción

Un conjunto numérico es un objeto matemático que posee elementos. Éstos elementos pertenecen al objeto como característica principal.

Los conjuntos se pueden expresar de dos maneras:

• Extensión: Se escriben todos los elementos

$A = \{2,4,6,...\}$

• Comprensión: Se escriben indicaciones para deducir elementos

$A = \{x/ x \in \mathbb{N} \land 2 \leq x\}$

Operaciones

Intersección de A y B

Una intersección es un conjunto formado por elementos comunes a los conjuntos A y B.

$A\cap B = \{x/ x \in A \land x \in B\}$

Unión de A y B

Una unión es un conjunto formado por elementos que pertenecen a A o B.

$A\cup B = \{x/ x \in A \lor x \in B\}$

Diferencia de A y B

Una diferencia es un conjunto formado por elementos que pertenecen a unos conjuntos pero no a otros.

$A - B = \{x/ x \in A \land x \notin B\}$

Conjunto vacío

Es un conjunto sin elementos $A = \emptyset = \{ \} \neq \{ \emptyset \}$

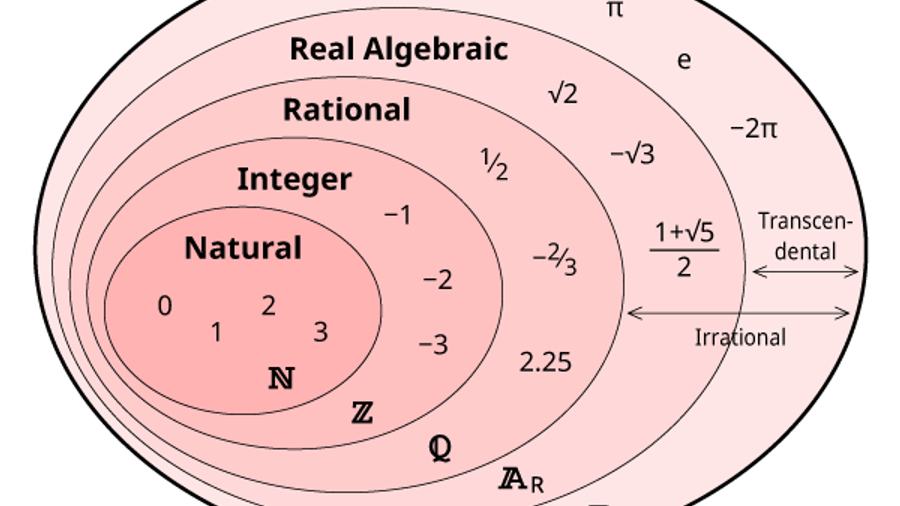
Conjuntos numéricos

• Naturales: Todos los números enteros positivos. Son los que usamos para contar.

$\mathbb{N} = \{ x \in \mathbb{Z} : x > 0 \}$

$\mathbb{N} = \{1,2,3,4,...\}$

• Enteros: Todos los números naturales más sus negativos.

$\mathbb{Z} = \{-3,-2,-1,\ 0,\ 1,\ 2,\ 3\}$

• Racionales: Es un conjunto formado por cocientes entre 2 enteros.

$\mathbb{Q} = \{x/ x=\dfrac{p}{q}, p \in \mathbb{Z},q \in \mathbb{Z} \land q \neq 0\}$

• Fraccionarios: Racionales que no son enteros

$\mathbb{F} = \mathbb{Q} - \mathbb{Z}$

$\mathbb{F} = \{x/ x=\dfrac{p}{q}, p \in \mathbb{Z},q \in \mathbb{Z} \land q \neq 0 \land x \notin \mathbb{Z} \}$

• Irracionales: Está formado por aquellos números que no pueden expresarse como cociente de números enteros (infinitos decimales no periódicos)

• Reales: Es la unión entre los números racionales e irracionales

Representación gráfica